A System Is Described By The Following Differential Equation

by

11.2: Basic First-order System Methods 11.3: Structure of Linear Systems 11.4: Matrix Exponential 11.5: The Eigenanalysis Method for x′ = Ax 11.6: Jordan Form and Eigenanalysis 11.7: Nonhomogeneous Linear Systems 11.8: Second-order Systems 11.9: Numerical Methods for Systems Linear systems. A linear system is a system of differential equa

Checking solutions to systems of equations | Khan Academy Wiki | Fandom

Aug 27, 2022The difference in form between Equation \refeq:10.1.15 and Equation \refeq:10.1.17, due to the way in which the unknowns are denoted in the two systems, isn’t important; Equation \refeq:10.1.17 is a first order system, in that each equation in Equation \refeq:10.1.17 expresses the first derivative of one of the unknown functions in a

Solved d? y(t) = Exercise 1. A system is described by the | Chegg.com
Source Image: chegg.com
Download Image

There is a generalizations of Abel’s Theorem for systems of linear differential equations. W dt = (p11 +p22+…pnn)W (5.4.6) (5.4.6) W d t = ( p 11 + p 22 +… p n n) W. The main theorem on uniqueness and existence of solutions of systems of differential equations also holds true. We state it below.

Studying for Differential Equations Final : r/math
Source Image: reddit.com
Download Image


Aquifer conditions, not irradiance determine the potential of photovoltaic energy for groundwater pumping across Africa | Communications Earth & Environment

Question A system is described by the following differential equation: \frac d^ 3 y d t^ 3+3 \frac d^ 2 y d t^ 2+5 \frac d y d t+y=\frac d^ 3 x d t^ 3+4 \frac d^ 2 x d t^ 2+6 \frac d x d t+8 x dt3d3y +3dt2d2y +5dtdy +y = dt3d3x +4 dt2d2x +6 dtdx +8x

Analogue computing: fun with differential equations - Chalkdust
Source Image: chalkdustmagazine.com
Download Image

A System Is Described By The Following Differential Equation

Question A system is described by the following differential equation: \frac d^ 3 y d t^ 3+3 \frac d^ 2 y d t^ 2+5 \frac d y d t+y=\frac d^ 3 x d t^ 3+4 \frac d^ 2 x d t^ 2+6 \frac d x d t+8 x dt3d3y +3dt2d2y +5dtdy +y = dt3d3x +4 dt2d2x +6 dtdx +8x
Consequently, a linear, time-invariant system specified by a linear con-stant-coefficient differential or difference equation must have its auxiliary Signals and Systems. 6-2. conditions consistent with that property. If, in fact, the system is causal in ad-dition to being linear and time-invariant, then the auxiliary conditions will correspond

Analogue computing: fun with differential equations – Chalkdust

Nov 16, 2022Systems of differential equations can be converted to matrix form and this is the form that we usually use in solving systems. Example 3 Convert the following system to matrix form. x′ 1 =4×1 +7×2 x′ 2 =−2×1−5×2 x ′ 1 = 4 x 1 + 7 x 2 x ′ 2 = − 2 x 1 − 5 x 2. Show Solution. Example 4 Convert the systems from Examples 1 and 2 into

Energies | Free Full-Text | A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications

Energies | Free Full-Text | A Comprehensive Review on a Virtual-Synchronous Generator: Topologies, Control Orders and Techniques, Energy Storages, and Applications
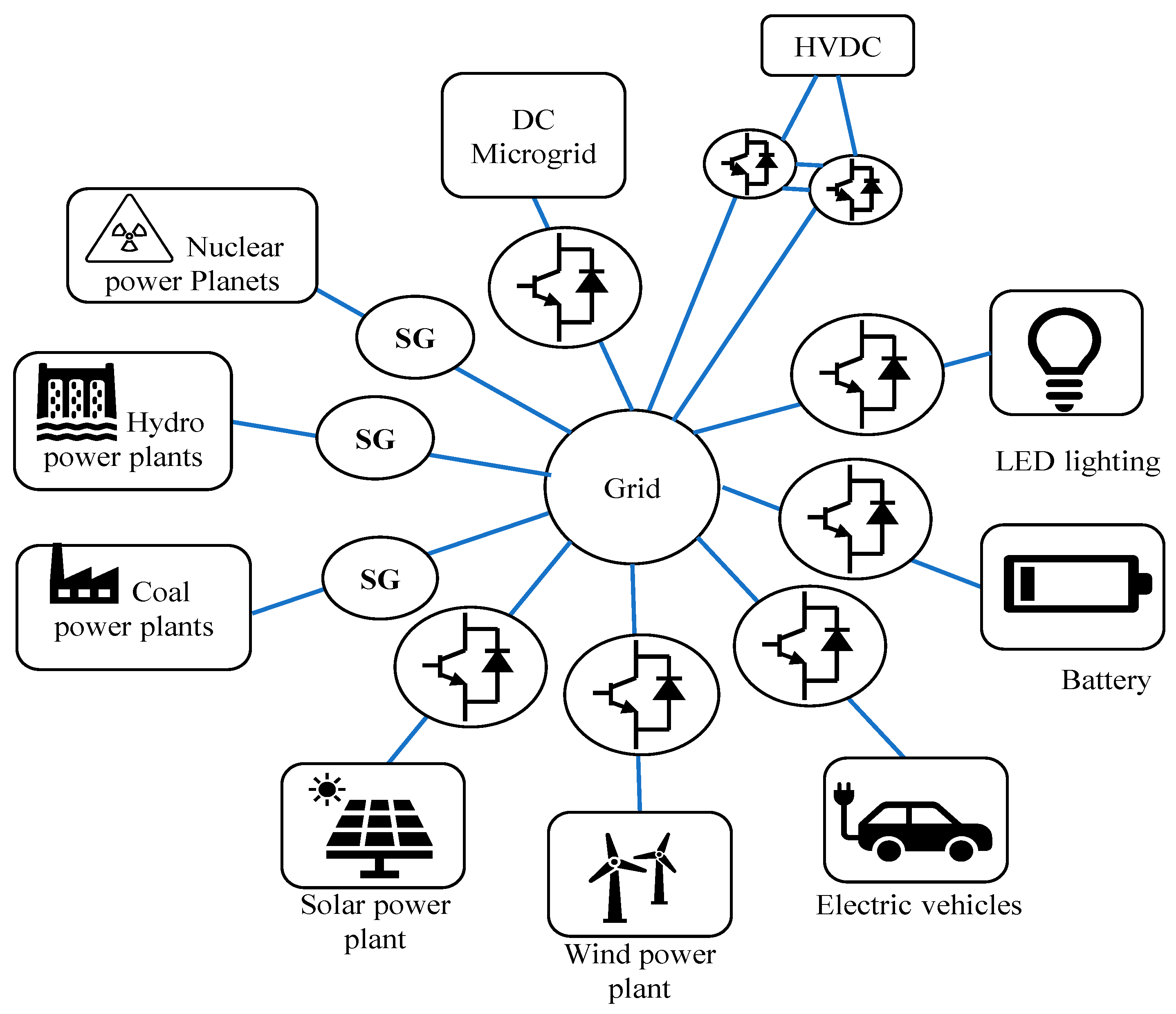
Source Image: mdpi.com
Download Image


The Intuition behind the Laplace Transform | by Son Cain | Intuition | Medium

Nov 16, 2022Systems of differential equations can be converted to matrix form and this is the form that we usually use in solving systems. Example 3 Convert the following system to matrix form. x′ 1 =4×1 +7×2 x′ 2 =−2×1−5×2 x ′ 1 = 4 x 1 + 7 x 2 x ′ 2 = − 2 x 1 − 5 x 2. Show Solution. Example 4 Convert the systems from Examples 1 and 2 into

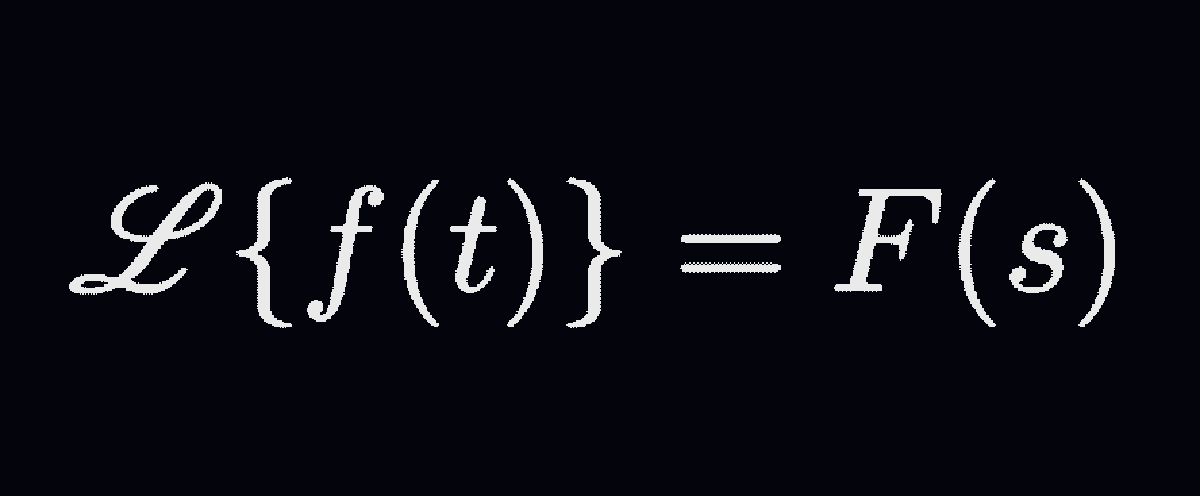
The Intuition behind the Laplace Transform | by Son Cain | Intuition | Medium
Source Image: medium.com
Download Image


Checking solutions to systems of equations | Khan Academy Wiki | Fandom

11.2: Basic First-order System Methods 11.3: Structure of Linear Systems 11.4: Matrix Exponential 11.5: The Eigenanalysis Method for x′ = Ax 11.6: Jordan Form and Eigenanalysis 11.7: Nonhomogeneous Linear Systems 11.8: Second-order Systems 11.9: Numerical Methods for Systems Linear systems. A linear system is a system of differential equa

Checking solutions to systems of equations | Khan Academy Wiki | Fandom
Source Image: khanacademy.fandom.com
Download Image


Aquifer conditions, not irradiance determine the potential of photovoltaic energy for groundwater pumping across Africa | Communications Earth & Environment

There is a generalizations of Abel’s Theorem for systems of linear differential equations. W dt = (p11 +p22+…pnn)W (5.4.6) (5.4.6) W d t = ( p 11 + p 22 +… p n n) W. The main theorem on uniqueness and existence of solutions of systems of differential equations also holds true. We state it below.

Aquifer conditions, not irradiance determine the potential of photovoltaic energy for groundwater pumping across Africa | Communications Earth & Environment
Source Image: nature.com
Download Image


NVIDIA Announces Modulus: A Framework for Developing Physics ML Models for Digital Twins | NVIDIA Technical Blog

We’ll say that A and f are continuous if their entries are continuous. If f = 0, then Equation 10.2.2 is homogeneous; otherwise, Equation 10.2.2 is nonhomogeneous. An initial value problem for Equation 10.2.2 consists of finding a solution of Equation 10.2.2 that equals a given constant vector. k = [k1 k2 ⋮ kn].

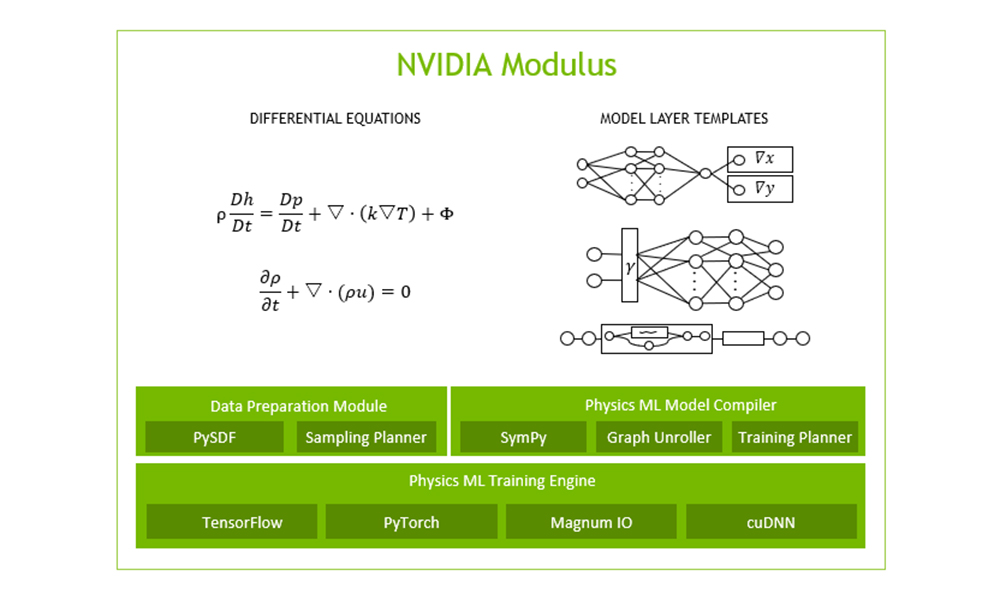
NVIDIA Announces Modulus: A Framework for Developing Physics ML Models for Digital Twins | NVIDIA Technical Blog
Source Image: developer.nvidia.com
Download Image


Problem on differential equation

Question A system is described by the following differential equation: \frac d^ 3 y d t^ 3+3 \frac d^ 2 y d t^ 2+5 \frac d y d t+y=\frac d^ 3 x d t^ 3+4 \frac d^ 2 x d t^ 2+6 \frac d x d t+8 x dt3d3y +3dt2d2y +5dtdy +y = dt3d3x +4 dt2d2x +6 dtdx +8x

Problem on differential equation
Source Image: mymathware.blogspot.com
Download Image


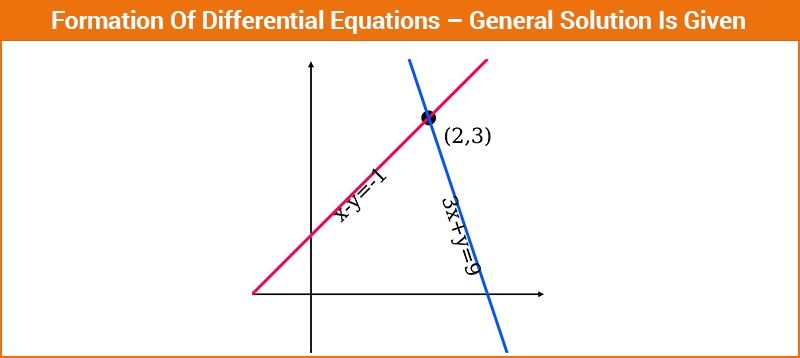
Formation of Differential Equations with General Solution

Consequently, a linear, time-invariant system specified by a linear con-stant-coefficient differential or difference equation must have its auxiliary Signals and Systems. 6-2. conditions consistent with that property. If, in fact, the system is causal in ad-dition to being linear and time-invariant, then the auxiliary conditions will correspond

Formation of Differential Equations with General Solution
Source Image: byjus.com
Download Image

The Intuition behind the Laplace Transform | by Son Cain | Intuition | Medium

Formation of Differential Equations with General Solution

Aug 27, 2022The difference in form between Equation \refeq:10.1.15 and Equation \refeq:10.1.17, due to the way in which the unknowns are denoted in the two systems, isn’t important; Equation \refeq:10.1.17 is a first order system, in that each equation in Equation \refeq:10.1.17 expresses the first derivative of one of the unknown functions in a

Aquifer conditions, not irradiance determine the potential of photovoltaic energy for groundwater pumping across Africa | Communications Earth & Environment Problem on differential equation

We’ll say that A and f are continuous if their entries are continuous. If f = 0, then Equation 10.2.2 is homogeneous; otherwise, Equation 10.2.2 is nonhomogeneous. An initial value problem for Equation 10.2.2 consists of finding a solution of Equation 10.2.2 that equals a given constant vector. k = [k1 k2 ⋮ kn].